#load grafify
library(grafify)Loading required package: ggplot2plot_scatterbox(Weights_long,
Diet,
Bodyweight)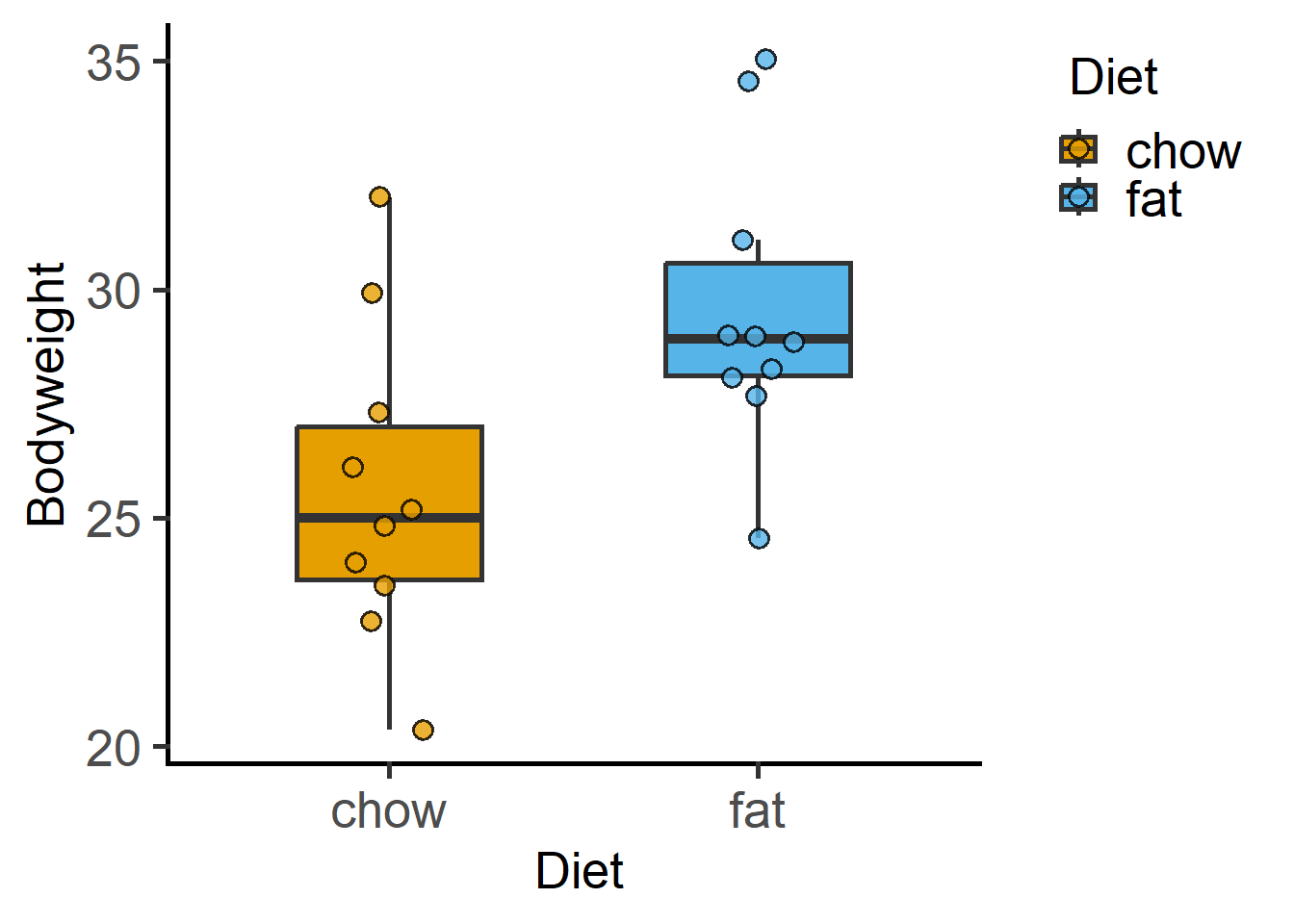
We respect your right to privacy. You can choose not to allow some types of cookies. Your cookie preferences will apply across our website.
We use cookies on our site to analyze our traffic, which may help with future research grant applications to support this website. Cookie Policy.
Created Oct 2022, Last updated: 08 October, 2025
This page has code for session 2 of BPI stats workshop. These exercises will only work if you have completed the pre-session items described here correctly. Go to the Session 1 instructions before these exercises.
ProjectCreate a project and work inside it to stay organised. You may continue in the project you created in session 1.
We will use data in grafify and the “Weights.xlsx” file we imported previously.
R prefers long data format for plotting. It is always easier to convert wide data table to long using the tidyr package as shown in an example here.
We will use Weights_long for exploratory graphs.
Loading required package: ggplot2
penguins has some rows with no data (NULL or NA), which we will remove for this session (to avoid certain errors – it is not OK to exclude data without good reason!).
Attaching package: 'palmerpenguins'The following objects are masked from 'package:datasets':
penguins, penguins_raw[1] 344 8#remove null data with na.omit
penguins <- na.omit(palmerpenguins::penguins)
dim(penguins) #table dimensions without null rows[1] 333 8tibble [333 × 8] (S3: tbl_df/tbl/data.frame)
$ species : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...
$ island : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...
$ bill_length_mm : num [1:333] 39.1 39.5 40.3 36.7 39.3 38.9 39.2 41.1 38.6 34.6 ...
$ bill_depth_mm : num [1:333] 18.7 17.4 18 19.3 20.6 17.8 19.6 17.6 21.2 21.1 ...
$ flipper_length_mm: int [1:333] 181 186 195 193 190 181 195 182 191 198 ...
$ body_mass_g : int [1:333] 3750 3800 3250 3450 3650 3625 4675 3200 3800 4400 ...
$ sex : Factor w/ 2 levels "female","male": 2 1 1 1 2 1 2 1 2 2 ...
$ year : int [1:333] 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...
- attr(*, "na.action")= 'omit' Named int [1:11] 4 9 10 11 12 48 179 219 257 269 ...
..- attr(*, "names")= chr [1:11] "4" "9" "10" "11" ...Let us look at the penguins data set in the palmerpenguins package by plotting “body_mass_g” vs “species” and “sex”.
#add another variable with faceting
plot_scatterbox(data = penguins,
xcol = species,
ycol = body_mass_g,
facet = sex,
fontsize = 14,
TextXAngle = 45)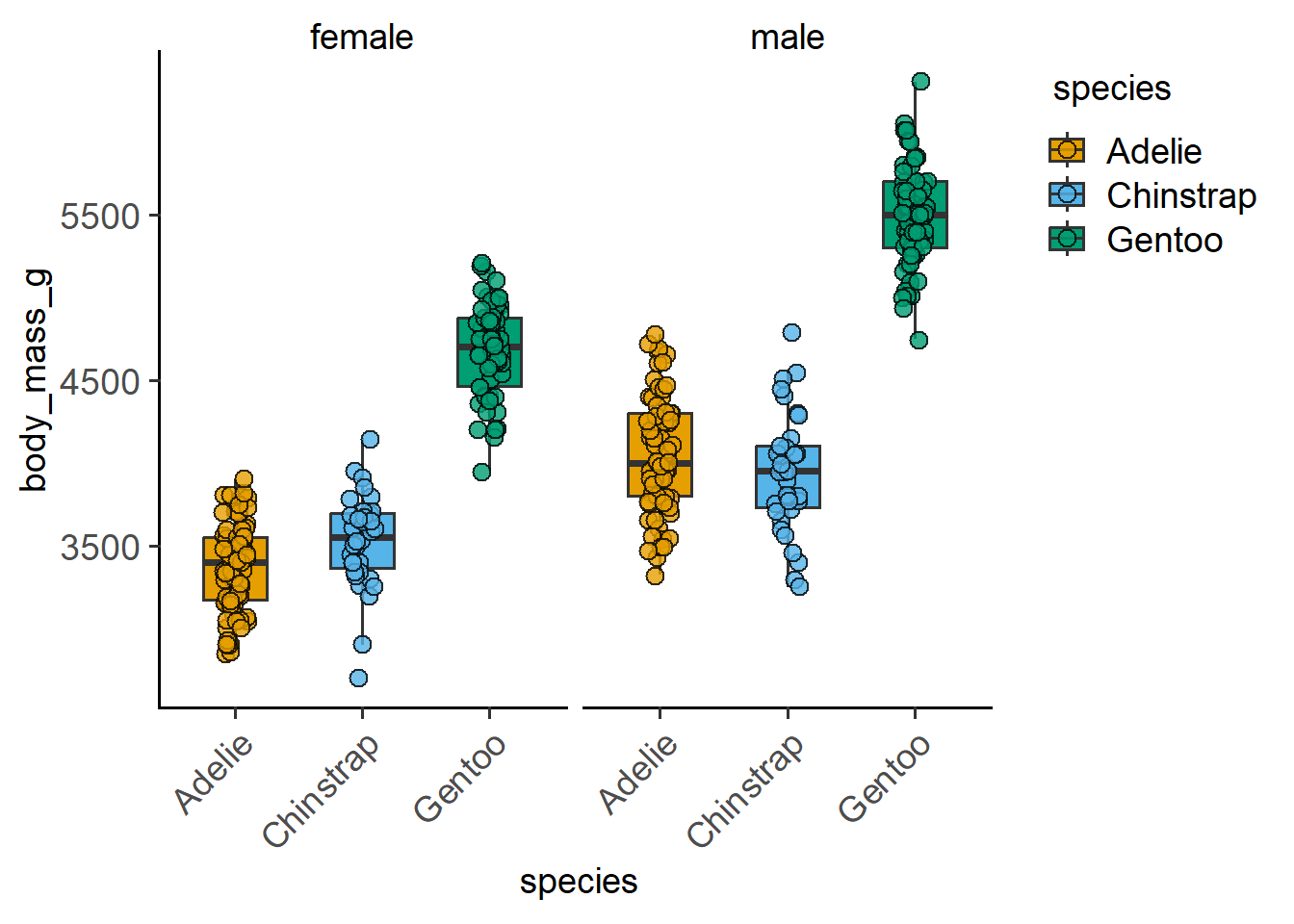
#add another variable with plot_4d
plot_4d_scatterbox(data = penguins,
xcol = species,
ycol = body_mass_g,
boxes = sex,
facet = island,
fontsize = 14,
TextXAngle = 45)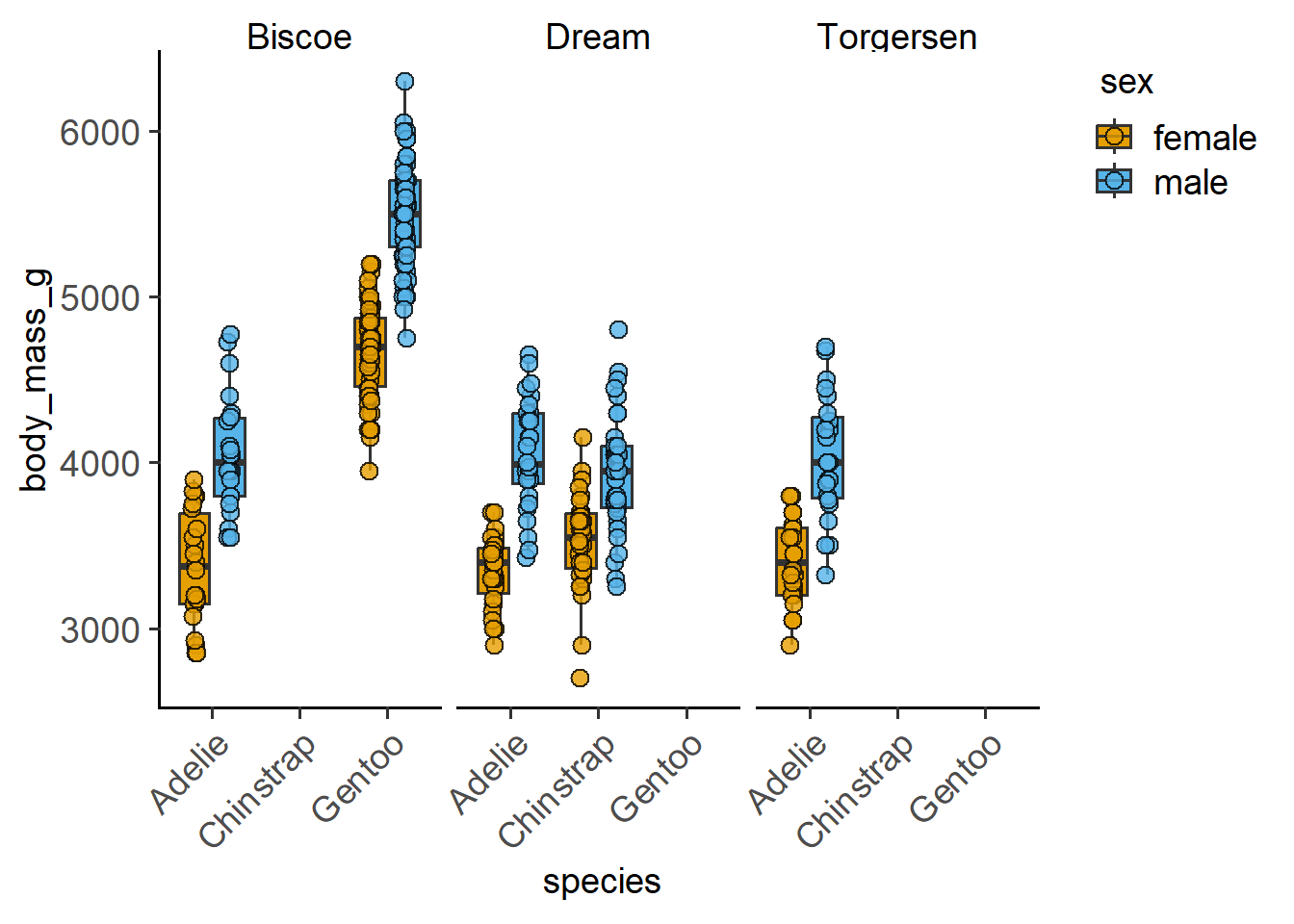
You can change the way the graph looks by tweaking arguments to the plot_* function.
You can change colours and tweak many parameters in these graphs:
We can also have another quantitative variable as another dimension.
#numeric x vs y plot1
plot_xy_CatGroup(penguins,
xcol = bill_length_mm,
ycol = bill_depth_mm,
CatGroup = species) 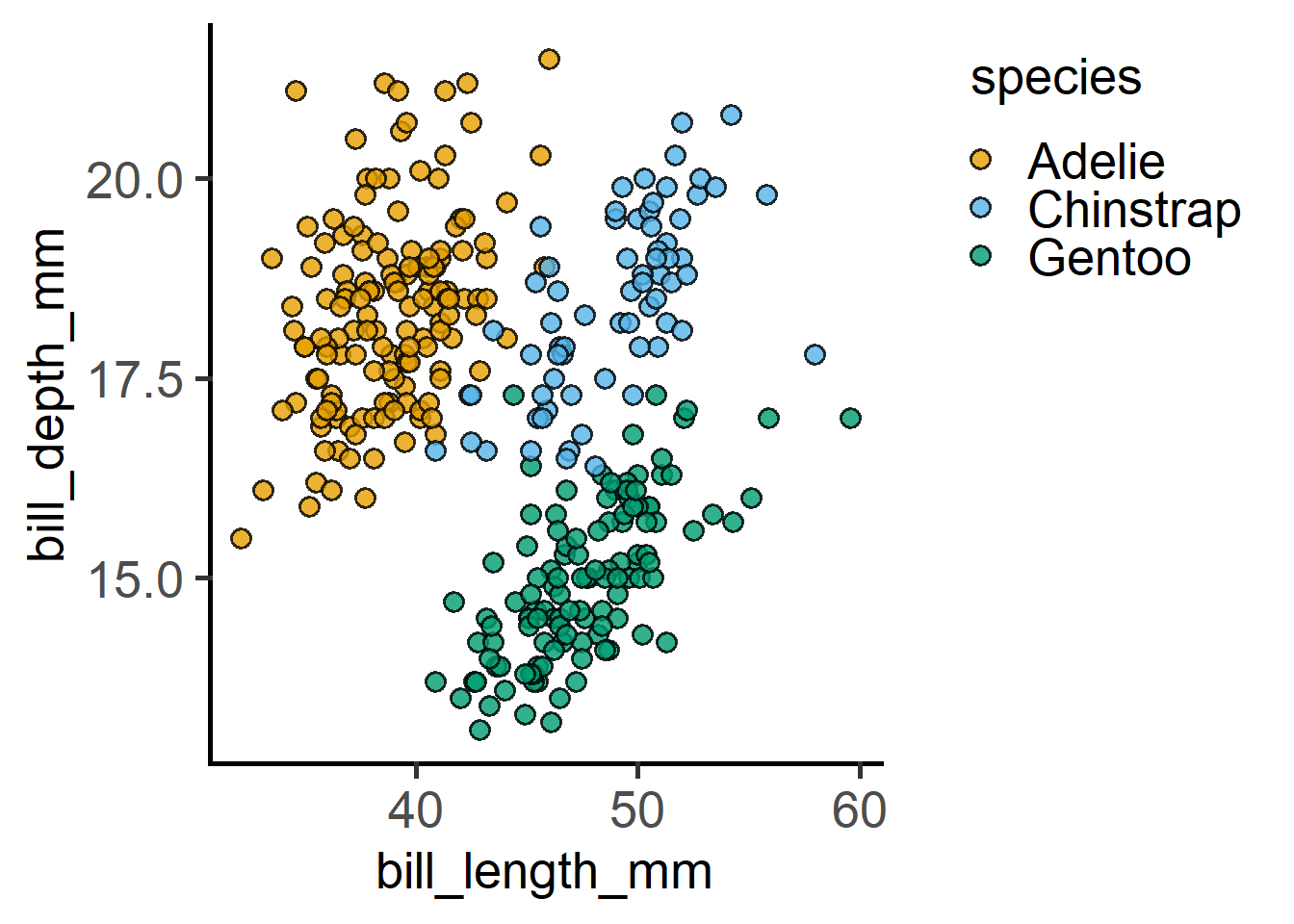
#numeric x vs y plot2
plot_xy_NumGroup(penguins,
xcol = bill_length_mm,
ycol = bill_depth_mm,
NumGroup = flipper_length_mm)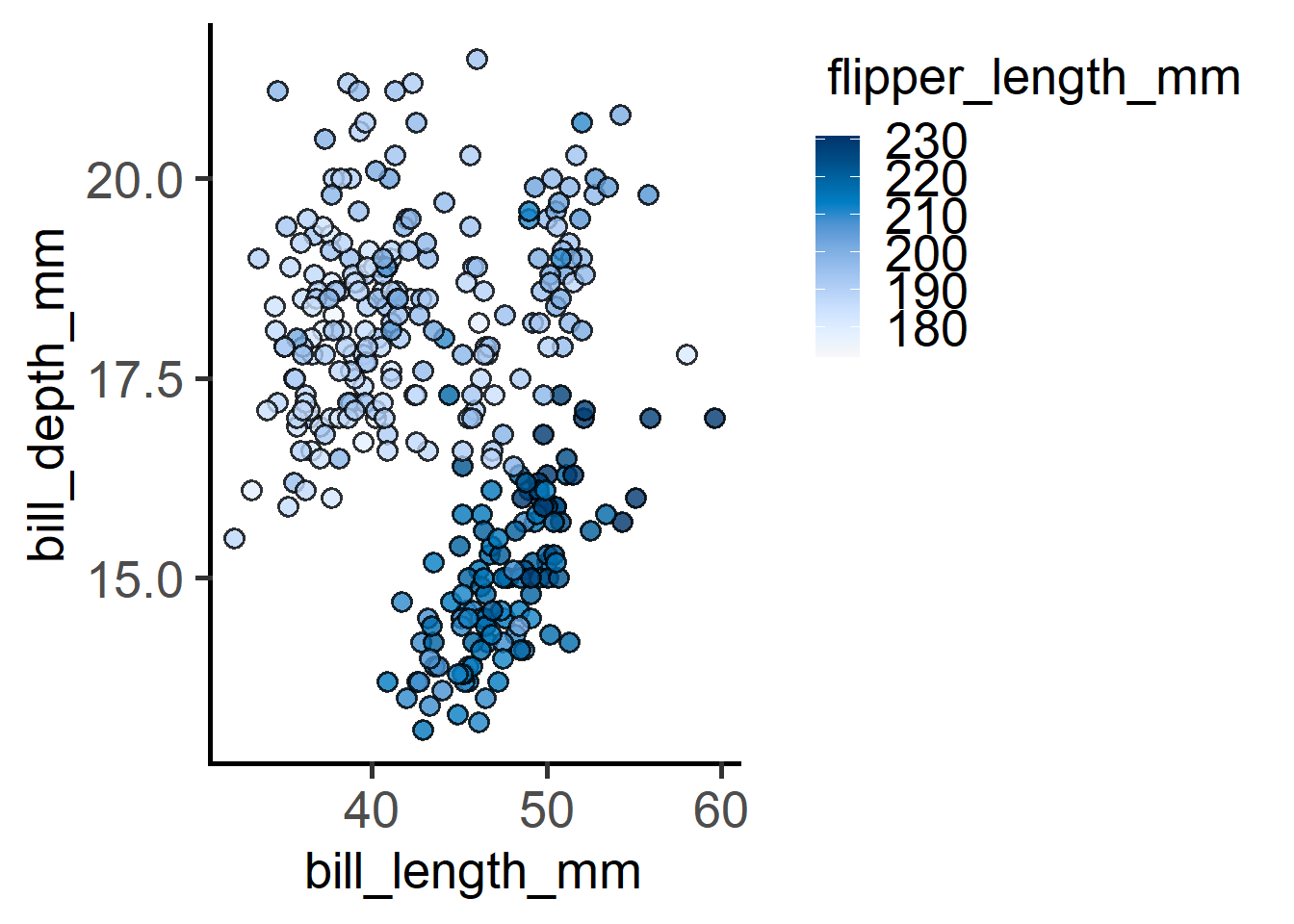
Data distributions can also be plotted.
With long data, we use the formula input, i.e., Y ~ X, where Y is the numeric variable or outcome or dependent variable (this is usually plotted in the Y-axis) and X is the categorical or discrete independent variable (usually on X-axis). The tilde sign ~ is a special character in R used for formula in linear regression. It indicates the variable on the left hand side is predicted by or varies with the variable(s) on right hand side.
#formula with long table
t.test(formula = Bodyweight ~ Diet, #formula input for t.test()
data = Weights_long)
Welch Two Sample t-test
data: Bodyweight by Diet
t = -2.7058, df = 17.892, p-value = 0.01453
alternative hypothesis: true difference in means between group chow and group fat is not equal to 0
95 percent confidence interval:
-7.1178367 -0.8941633
sample estimates:
mean in group chow mean in group fat
25.603 29.609 With wide tables, the $ operator is used to point to the two columns containing data to be compared.
Welch Two Sample t-test
data: Weights$chow and Weights$fat
t = -2.7058, df = 17.892, p-value = 0.01453
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-7.1178367 -0.8941633
sample estimates:
mean of x mean of y
25.603 29.609 Therefore, if the null hypothesis was true, the chance of observing a test statistic at least as extreme as 2.7058 is 0.01453. Given that we usually set
A t test is reliable only if the data in both groups are approximately normally distributed. In reality, with few independently performed experiments (i.e., small sample size), this may be difficult to test. But a strong deviation from normal distribution is a “red flag” (i.e., you should consider data transformations).
One way to check approximate normal distributions is to plot a QQ plot of both groups before performing the test.
Note: this is only the case for t tests; in ANOVAs (when there are more than 3 groups present), the normality of the residuals from the model should be tested rather than that of the raw data. See the section on t test as a linear model for further details.
Student’s t test is only appropriate when you are comparing exactly two groups. It is not correct to use multiple t tests when you have multiple groups to compare – you should use ANOVAs. In the statistics section of Methods and/or figure legends, you must report the test, the P value, whether you performed a one- or two-tailed test and whether you had independent or matched data. In the Methods section, you should also mention how experiments were designed, any data transformation and diagnostics performed on model residuals. More formally, the result is reported as follows (but this is uncommon in biology journals): The result of a two-tailed independent group t test were as follows: t (17.892) = -2.71; P = 0.01453. The t statistic and the degrees of freedom give an idea of the sample size and effect size, which is the basis for obtaining the P value and is therefore more informative.
Let’s first get the mean and SD of the two groups and look at the chance of getting a similar “significant” result with 10 independent draws from the same distributions.
Diet Bodyweight.Mean Bodyweight.Median Bodyweight.SD Bodyweight.Count
1 chow 25.603 25.005 3.436659 10
2 fat 29.609 28.915 3.179509 10The mean
Let’s try and see how much variability we have in t tests for 10 random numbers drawn from these distributions (i.e., normal distributions with with these mean and SD) using the rnom function.
#rnorm gives random variates from normal distribution
t.test(x = rnorm(n = 10, #number of variates
mean = 25.604, #mean
sd = 3.5), #sd
y = rnorm(n = 10,
mean = 29.609,
sd = 3.18))
Welch Two Sample t-test
data: rnorm(n = 10, mean = 25.604, sd = 3.5) and rnorm(n = 10, mean = 29.609, sd = 3.18)
t = -2.8808, df = 17.273, p-value = 0.01025
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-7.434617 -1.152975
sample estimates:
mean of x mean of y
26.72564 31.01944 #repeat 10 times with replicate()
#get P values with $p.value
replicate(t.test(x = rnorm(n = 10,
mean = 25.604,
sd = 3.5),
y = rnorm(n = 10,
mean = 29.609,
sd = 3.18))$p.value,
n = 10) [1] 0.0337802737 0.0010665313 0.0232023877 0.0007983586 0.0324007736
[6] 0.0919763717 0.0057479152 0.0062936697 0.0269941207 0.0002506252From these 10 tests, how many have P <
The idea is to start with a sufficiently large sample size so we can correctly reject the null hypothesis (when it is false) at least 80 % of repeated sampling. This means a power of 0.8 (i.e., false negative rate
To calculate power, we need to know Cohen’s effect size d. Below we calculate Cohen’s effect size d by hand (difference between the means/pooled SD). The effectsize package has a convenient function to do this for more complex cases (e.g., when the number of both groups is not equal). See an example of how to use it here.
[1] -1.217629#alternative method
#install the package pwr first
library(pwr) #load the library
#formula input like t.test()
effectsize::cohens_d(Bodyweight ~ Diet,
data = Weights_long)Cohen's d | 95% CI
--------------------------
-1.21 | [-2.16, -0.24]
- Estimated using pooled SD.Cohen's d | 95% CI
--------------------------
-1.21 | [-2.16, -0.24]
- Estimated using pooled SD.#use the value in the next step
pwr.t.test(n = NULL, #we want to estimate this
d = -1.21, #effect size
sig.level = 0.05, #desired alpha
power = 0.8) #desired power (1-beta)
Two-sample t test power calculation
n = 11.76412
d = 1.21
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* groupIf you had known the means and SDs before hand (e.g., in a small pilot experiment), you should design the main experiment with 12 mice per group for 80 % power for the experiment. Let’s repeat the simulated t test above with n = 12 to check for increased power as compared to n = 10.
This is an exercise for you. The above examples used code for groups with independent sampling. These data are from matched mice!
Repeat the above t tests and power analyses for paired or matched data. You could use the wide table for the t.test and the cohen_d functions with an additional argument paired = TRUE in both functions.
How do the results differ? Is the sample size different if the experiment was designed with independent mice or matched mice?
In R linear models (straight lines) can be fit with the function lm. In grafify, this is done with simple_model for independent groups and mixed_model for paired or matched data. See the code below and identify the formula in the outputs.
#for independent groups
simple_model(data = Weights_long,
Y_value = "Bodyweight",
Fixed_Factor = "Diet")
Call:
lm(formula = Bodyweight ~ Diet, data = Weights_long)
Coefficients:
(Intercept) Dietfat
25.603 4.006 #for matched data
mixed_model(data = Weights_long,
Y_value = "Bodyweight",
Fixed_Factor = "Diet",
Random_Factor = "Mouse")The new argument `AvgRF` is set to TRUE by default in >=5.0.0). Response variable is averaged over levels of Fixed and Random factors. Use help for details.Linear mixed model fit by REML ['lmerModLmerTest']
Formula: Bodyweight ~ Diet + (1 | Mouse)
Data: Weights_long (AvgRF)
REML criterion at convergence: 97.4276
Random effects:
Groups Name Std.Dev.
Mouse (Intercept) 2.024
Residual 2.619
Number of obs: 20, groups: Mouse, 10
Fixed Effects:
(Intercept) Dietfat
25.603 4.006 Note that the Intercept is the mean of group 1 (chosen alphabetically unless reordered by hand), and Dietfat is the slope, i.e., the difference between the two means. Compare the values of the Intercept and Dietfat (group 2) with the t.test results above. For diagnostics and post-hoc tests, we will need to save the linear model object.
#save the model
weights_model <- simple_model(data = Weights_long,
Y_value = "Bodyweight",
Fixed_Factor = "Diet")
#use summary() to look at it
summary(weights_model)
Call:
lm(formula = Bodyweight ~ Diet, data = Weights_long)
Residuals:
Min 1Q Median 3Q Max
-5.243 -1.667 -0.694 1.538 6.417
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 25.603 1.047 24.456 2.92e-15 ***
Dietfat 4.006 1.481 2.706 0.0145 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.311 on 18 degrees of freedom
Multiple R-squared: 0.2891, Adjusted R-squared: 0.2496
F-statistic: 7.321 on 1 and 18 DF, p-value: 0.01447#similarly save the mixed effectsmodel
weights_mixed_model <- mixed_model(data = Weights_long,
Y_value = "Bodyweight",
Fixed_Factor = "Diet",
Random_Factor = "Mouse")The new argument `AvgRF` is set to TRUE by default in >=5.0.0). Response variable is averaged over levels of Fixed and Random factors. Use help for details.summary() shows the full details of the linear model object in R. It has the t statistic for the slope (Dietfat) and the associated P value.
In linear models, the null hypothesis is that slope = 0 i.e., the means of the two groups is the same and a line through the means is parallel to the X-axis. The alternative hypothesis is that the slope != 0 (not equal to 0), i.e., a line joining the two means is not parallel to X with either a positive or negative slope. Do we have evidence to reject the null hypothesis?
Before answering the above question and accepting the result of the test, we must diagnose the model, i.e., ask whether the straight line is a good fit to the data. If the line is a good fit, the residuals of the model should be approximately normally distributed.
We can then get the P value for the slope in an ANOVA table format. For balanced designs, the ANOVA F statistic is the square of the t statistic.
Anova Table (Type II tests)
Response: Bodyweight
Sum Sq Mean sq Df F value Pr(>F)
Diet 80.24 80.24 1 7.3212 0.01447 *
Residuals 197.28 10.96 18
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1As an exercise,
mixed_modelmixed_anova functions with Random_Factor = "Mouse" argument.Look closely at the results and answer:
simple_model result above?Question: did our experimental design with matched mice lead to increased power or should we have used different sets of mice? Which of the two is compatible with 3Rs?
Let’s look at the data_1w_death table from the grafify package.
'data.frame': 15 obs. of 3 variables:
$ Experiment: Factor w/ 5 levels "Exp_1","Exp_2",..: 1 1 1 2 2 2 3 3 3 4 ...
$ Genotype : Factor w/ 3 levels "WT","KO_1","KO_2": 1 2 3 1 2 3 1 2 3 1 ...
$ Death : num 25.01 1.82 14.29 16.54 2.13 ...Here are further instructions for ANOVAs as linear models.
#linear model
lm_1w_1 <- simple_model(data_1w_death,
Y_value = "Death",
Fixed_Factor = "Genotype")
#model summary includes details
summary(lm_1w_1)
Call:
lm(formula = Death ~ Genotype, data = data_1w_death)
Residuals:
Min 1Q Median 3Q Max
-7.9834 -1.5226 0.0159 2.4960 6.5997
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 24.526 1.830 13.403 1.40e-08 ***
GenotypeKO_1 -22.586 2.588 -8.727 1.53e-06 ***
GenotypeKO_2 -4.699 2.588 -1.816 0.0945 .
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.092 on 12 degrees of freedom
Multiple R-squared: 0.8761, Adjusted R-squared: 0.8554
F-statistic: 42.41 on 2 and 12 DF, p-value: 3.624e-06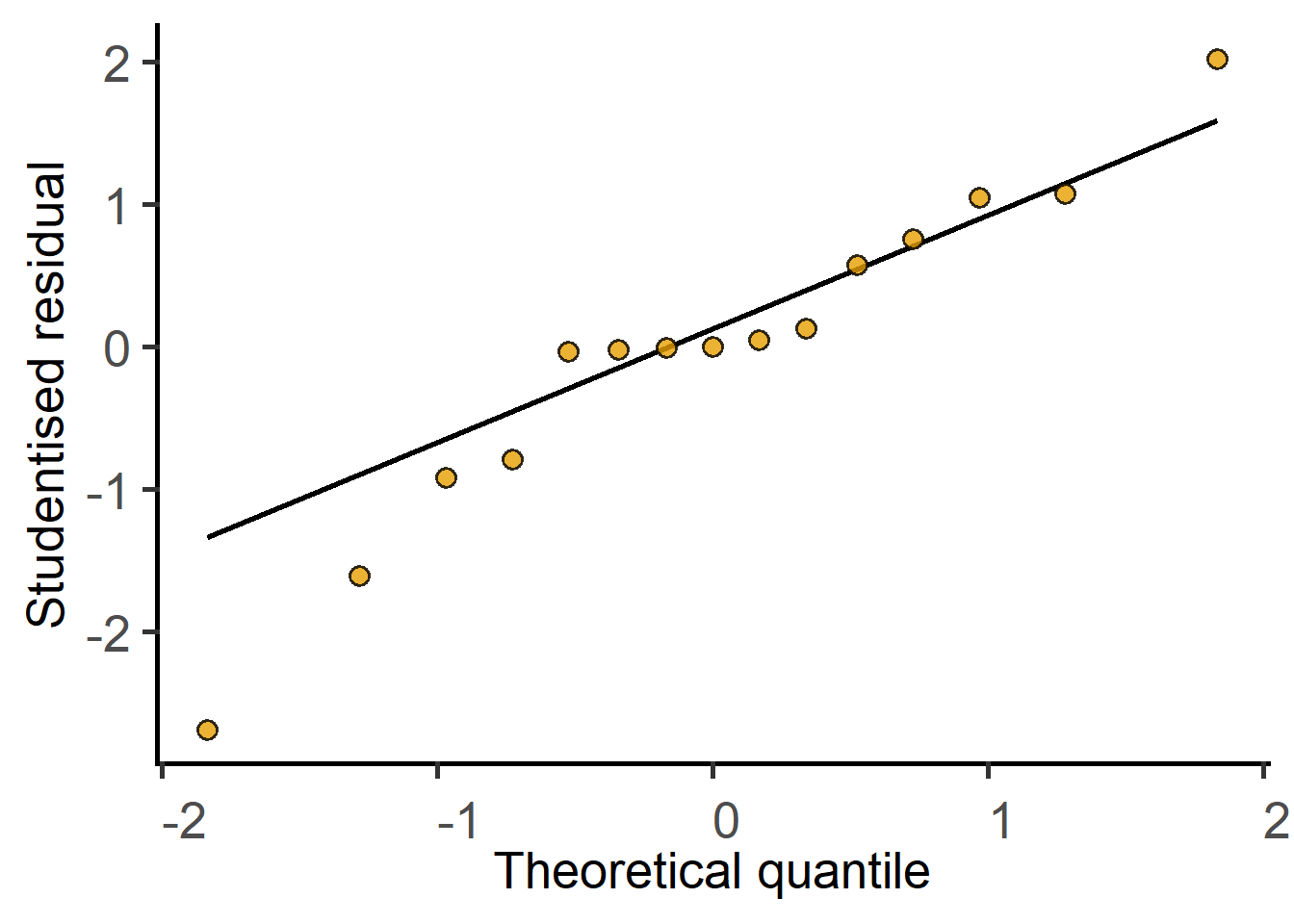
Anova Table (Type II tests)
Response: Death
Sum Sq Mean sq Df F value Pr(>F)
Genotype 1420.21 710.10 2 42.412 3.624e-06 ***
Residuals 200.91 16.74 12
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1These data are from randomised block designs, where each experiment is a block. Here are further instructions for linear mixed effects models.
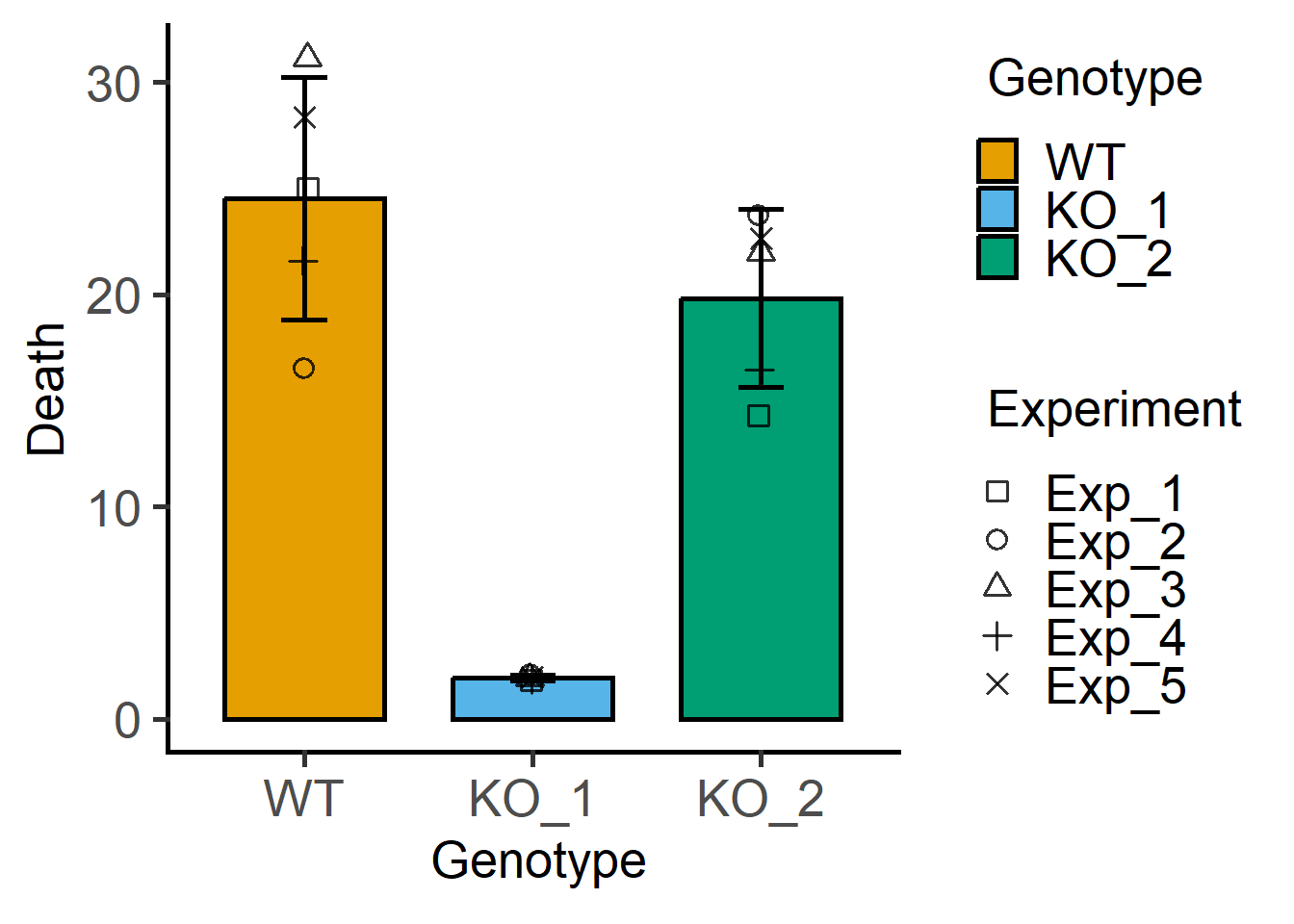
#explore further
#plot of each experiment
plot_befafter_box(data_1w_death,
xcol = Genotype,
ycol = Death,
match = Experiment)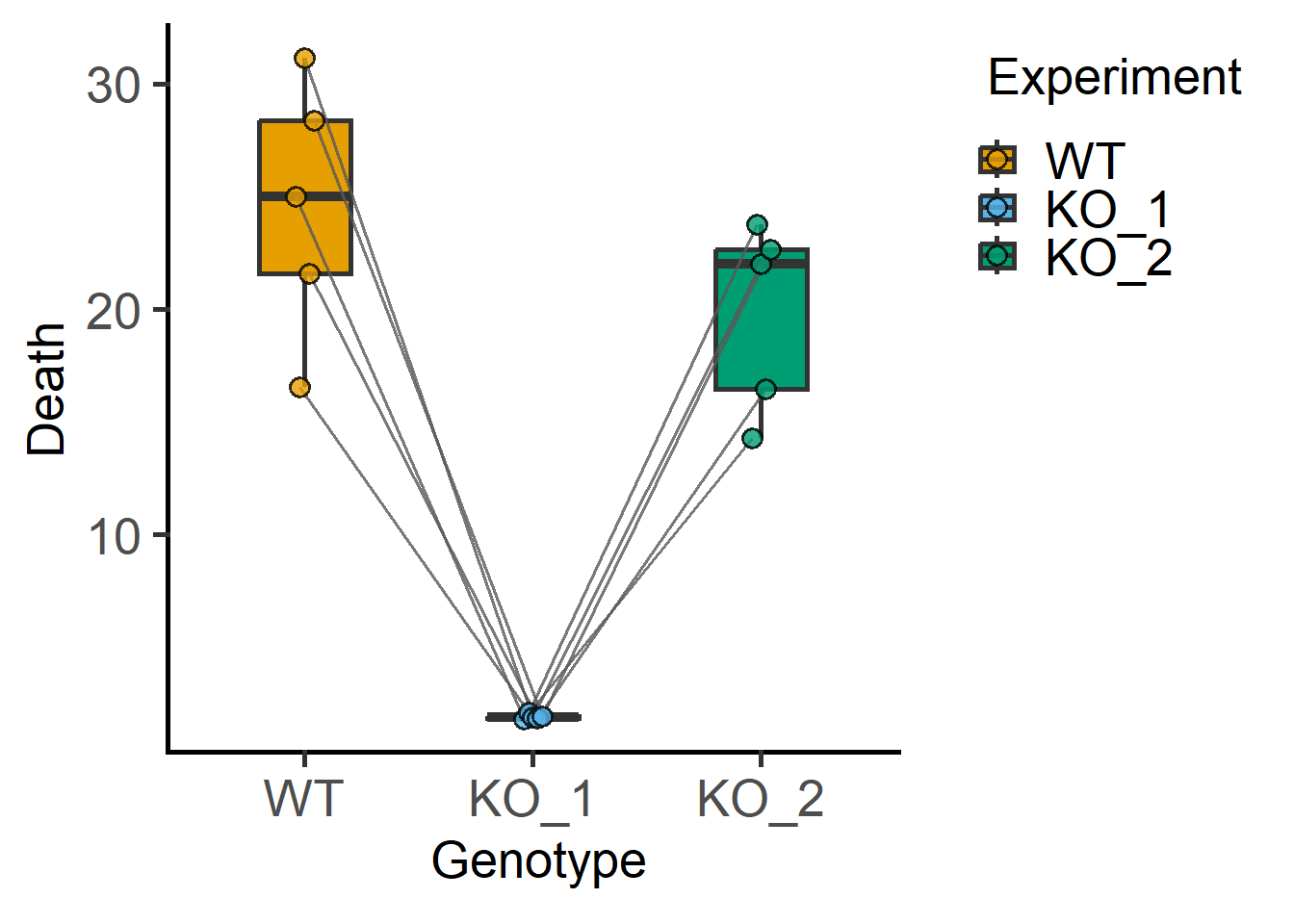
#fit a mixed effects model
mlm_1w_1 <- mixed_model(data_1w_death,
Y_value = "Death",
Fixed_Factor = "Genotype",
Random_Factor = "Experiment")The new argument `AvgRF` is set to TRUE by default in >=5.0.0). Response variable is averaged over levels of Fixed and Random factors. Use help for details.Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: Death ~ Genotype + (1 | Experiment)
Data: data_1w_death (AvgRF)
REML criterion at convergence: 72.7
Scaled residuals:
Min 1Q Median 3Q Max
-1.95132 -0.36509 -0.00545 0.60096 1.60534
Random effects:
Groups Name Variance Std.Dev.
Experiment (Intercept) 0.09695 0.3114
Residual 16.64594 4.0799
Number of obs: 15, groups: Experiment, 5
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 24.526 1.830 11.999 13.403 1.40e-08 ***
GenotypeKO_1 -22.586 2.580 7.999 -8.753 2.27e-05 ***
GenotypeKO_2 -4.699 2.580 7.999 -1.821 0.106
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) GnKO_1
GenotypKO_1 -0.705
GenotypKO_2 -0.705 0.500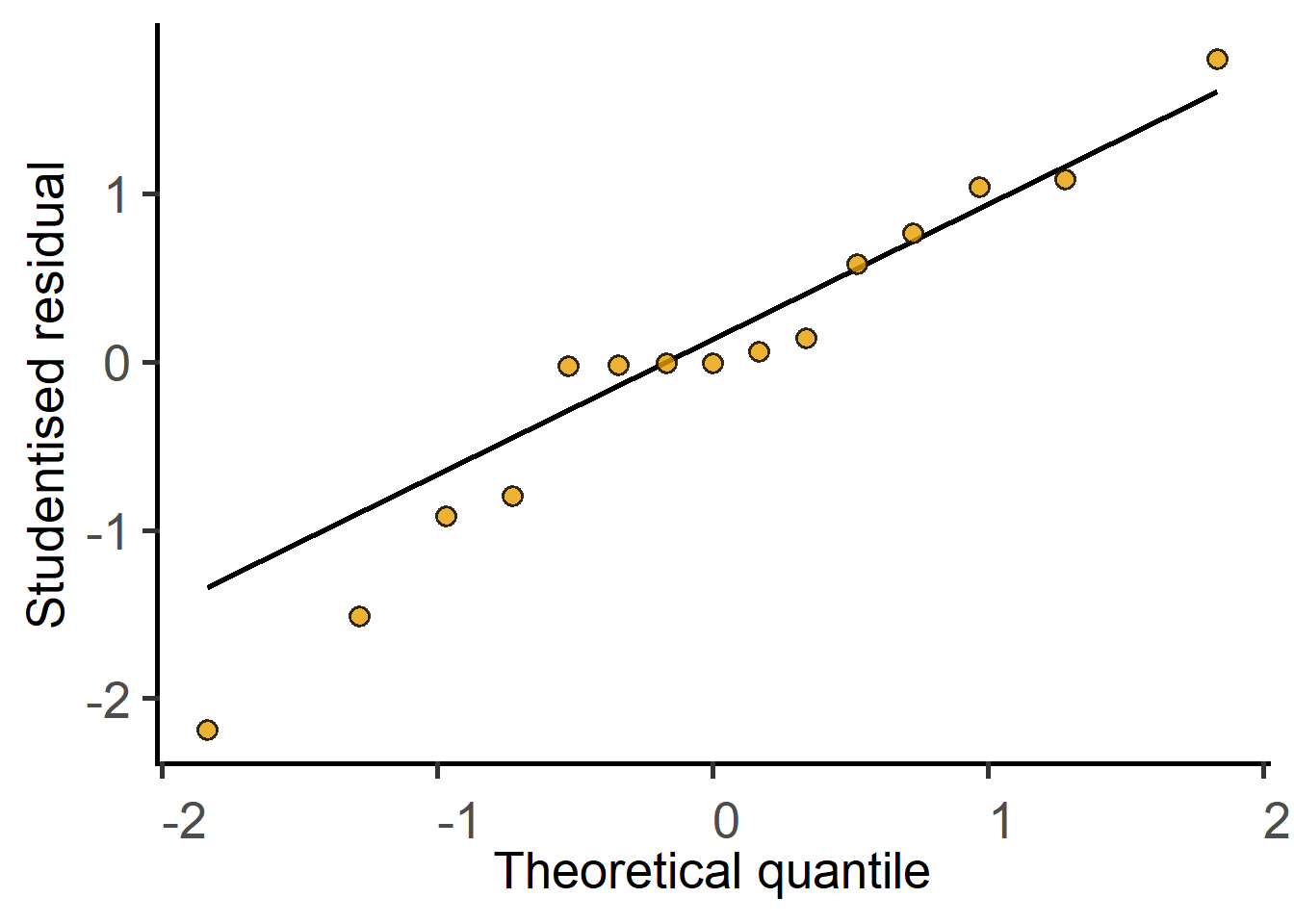
#ANOVA table
mixed_anova(data_1w_death,
Y_value = "Death",
Fixed_Factor = "Genotype",
Random_Factor = "Experiment")The new argument `AvgRF` is set to TRUE by default in >=5.0.0). Response variable is averaged over levels of Fixed and Random factors. Use help for details.Type II Analysis of Variance Table with Kenward-Roger's method
Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
Genotype 1420.2 710.1 2 8 42.659 5.401e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The data_2w_Festing data table is available in grafify package.
'data.frame': 16 obs. of 4 variables:
$ Block : Factor w/ 2 levels "A","B": 1 1 1 1 1 1 1 1 2 2 ...
$ Treatment: Factor w/ 2 levels "Control","Treated": 1 2 1 2 1 2 1 2 1 2 ...
$ Strain : Factor w/ 4 levels "129/Ola","A/J",..: 4 4 3 3 2 2 1 1 4 4 ...
$ GST : int 444 614 423 625 408 856 447 719 764 831 ...Plot GST vs the two factors “Strain” and “Treatment”. The question we’re addressing is whether GST levels depend on treatment across the strains of mice.
This is a randomised block design, which we will analyse with mixed effects analyses in grafify as a random intercepts linear model.
mlm_2w <- mixed_model(data_2w_Festing,
Y_value = "GST",
Fixed_Factor = c("Strain", "Treatment"),
Random_Factor = "Block")The new argument `AvgRF` is set to TRUE by default in >=5.0.0). Response variable is averaged over levels of Fixed and Random factors. Use help for details.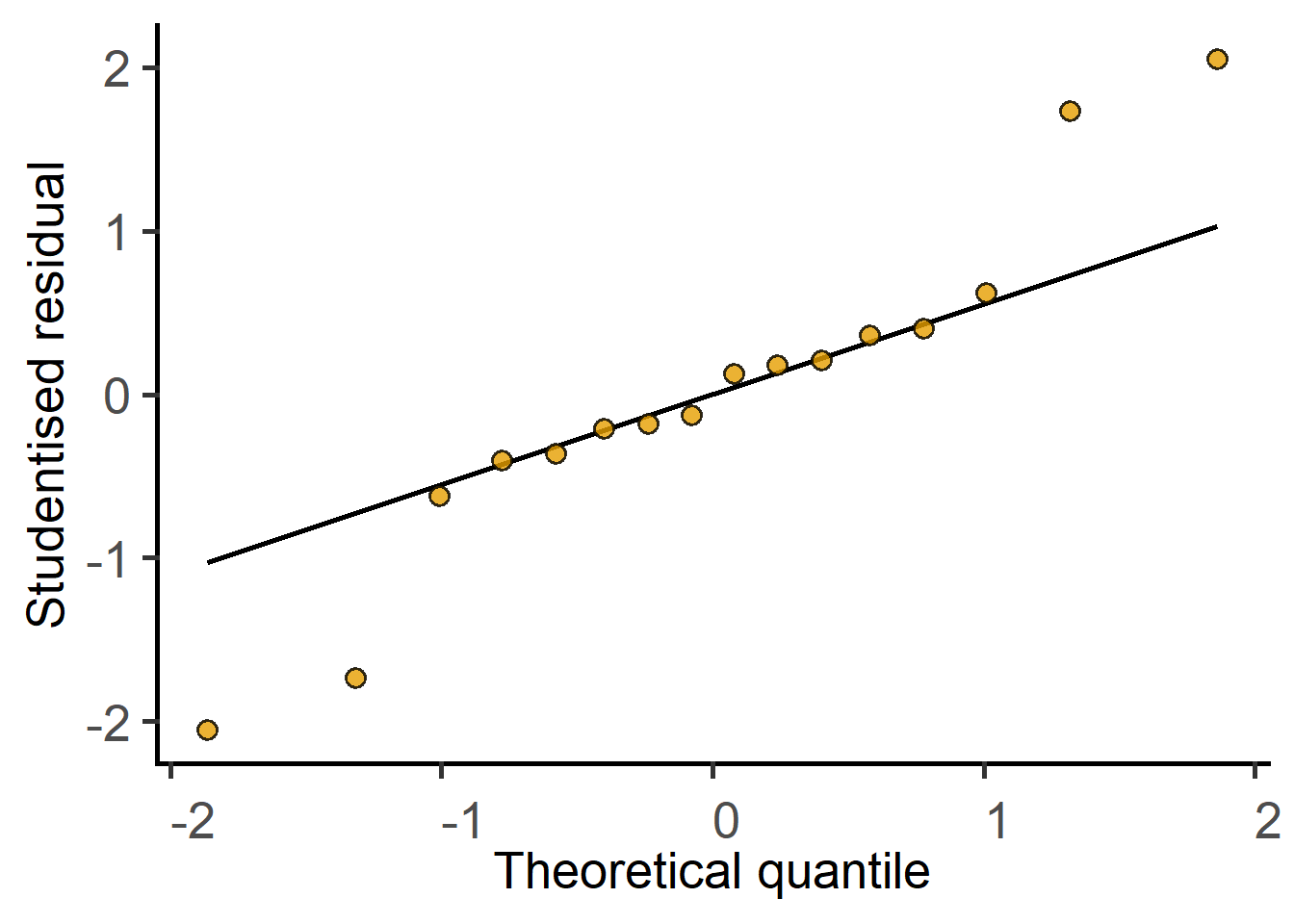
Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: GST ~ Strain * Treatment + (1 | Block)
Data: data_2w_Festing (AvgRF)
REML criterion at convergence: 95.9
Scaled residuals:
Min 1Q Median 3Q Max
-1.3603 -0.2462 0.0000 0.2462 1.3603
Random effects:
Groups Name Variance Std.Dev.
Block (Intercept) 15162 123.14
Residual 2957 54.38
Number of obs: 16, groups: Block, 2
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 526.500 95.183 1.356 5.531 0.06830 .
StrainA/J -18.000 54.381 7.000 -0.331 0.75033
StrainBALB/C -22.000 54.381 7.000 -0.405 0.69788
StrainNIH 77.500 54.381 7.000 1.425 0.19714
TreatmentTreated 216.000 54.381 7.000 3.972 0.00538 **
StrainA/J:TreatmentTreated 204.500 76.906 7.000 2.659 0.03251 *
StrainBALB/C:TreatmentTreated -17.000 76.906 7.000 -0.221 0.83136
StrainNIH:TreatmentTreated -97.500 76.906 7.000 -1.268 0.24541
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) StrA/J StBALB/C StrNIH TrtmnT SA/J:T SBALB/C:
StrainA/J -0.286
StranBALB/C -0.286 0.500
StrainNIH -0.286 0.500 0.500
TretmntTrtd -0.286 0.500 0.500 0.500
StrnA/J:TrT 0.202 -0.707 -0.354 -0.354 -0.707
StBALB/C:TT 0.202 -0.354 -0.707 -0.354 -0.707 0.500
StrnNIH:TrT 0.202 -0.354 -0.354 -0.707 -0.707 0.500 0.500 #ANOVA table
mixed_anova(data_2w_Festing,
Y_value = "GST",
Fixed_Factor = c("Strain", "Treatment"),
Random_Factor = "Block")The new argument `AvgRF` is set to TRUE by default in >=5.0.0). Response variable is averaged over levels of Fixed and Random factors. Use help for details.Type II Analysis of Variance Table with Kenward-Roger's method
Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
Strain 28613 9538 3 7 3.2252 0.09144 .
Treatment 227529 227529 1 7 76.9394 5.041e-05 ***
Strain:Treatment 49591 16530 3 7 5.5897 0.02832 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Functions in grafify can do this along with false-discovery rate based correction for multiple comparisons (as default).
For the one-way ANOVA analyses above, let’s compare whether KO1 and KO2 are statistically different from WT. We consider the WT level to be the ‘reference’ level, and use posthoc_vsRef, which requires the fitted linear model and factor name(s).
#default Ref_level = 1
#alphabetically the first level
#unless reordered with factor()
posthoc_vsRef(Model = mlm_1w_1,
Fixed_Factor = "Genotype")$emmeans
Genotype emmean SE df lower.CL upper.CL
WT 24.53 1.83 12 20.54 28.51
KO_1 1.94 1.83 12 -2.05 5.93
KO_2 19.83 1.83 12 15.84 23.81
Degrees-of-freedom method: kenward-roger
Confidence level used: 0.95
$contrasts
contrast estimate SE df t.ratio p.value
KO_1 - WT -22.6 2.58 8 -8.753 <.0001
KO_2 - WT -4.7 2.58 8 -1.821 0.1061
Degrees-of-freedom method: kenward-roger
P value adjustment: fdr method for 2 tests $emmeans
Genotype emmean SE df lower.CL upper.CL
WT 24.53 1.83 12 20.54 28.51
KO_1 1.94 1.83 12 -2.05 5.93
KO_2 19.83 1.83 12 15.84 23.81
Degrees-of-freedom method: kenward-roger
Confidence level used: 0.95
$contrasts
contrast estimate SE df t.ratio p.value
WT - KO_1 22.6 2.58 8 8.753 0.0001
WT - KO_2 4.7 2.58 8 1.821 0.1061
KO_1 - KO_2 -17.9 2.58 8 -6.932 0.0002
Degrees-of-freedom method: kenward-roger
P value adjustment: fdr method for 3 tests For the two-way ANOVA analyses above, let’s compare whether each Strain is affected by Treatment. For this we will use posthoc_Levelwise (e.g., to test whether GST at each level of Treatment has an effect at each level of Strain).
$emmeans
Strain = 129/Ola:
Treatment emmean SE df lower.CL upper.CL
Control 526 95.2 1.36 -140.0 1193
Treated 742 95.2 1.36 76.0 1409
Strain = A/J:
Treatment emmean SE df lower.CL upper.CL
Control 508 95.2 1.36 -158.0 1175
Treated 929 95.2 1.36 262.5 1595
Strain = BALB/C:
Treatment emmean SE df lower.CL upper.CL
Control 504 95.2 1.36 -162.0 1171
Treated 704 95.2 1.36 37.0 1370
Strain = NIH:
Treatment emmean SE df lower.CL upper.CL
Control 604 95.2 1.36 -62.5 1270
Treated 722 95.2 1.36 56.0 1389
Degrees-of-freedom method: kenward-roger
Confidence level used: 0.95
$contrasts
Strain = 129/Ola:
contrast estimate SE df t.ratio p.value
Control - Treated -216 54.4 7 -3.972 0.0054
Strain = A/J:
contrast estimate SE df t.ratio p.value
Control - Treated -420 54.4 7 -7.733 0.0001
Strain = BALB/C:
contrast estimate SE df t.ratio p.value
Control - Treated -199 54.4 7 -3.659 0.0081
Strain = NIH:
contrast estimate SE df t.ratio p.value
Control - Treated -118 54.4 7 -2.179 0.0657
Degrees-of-freedom method: kenward-roger One-way or factorial (two or more factors) ANOVAs used when there are more than two groups to compare. In the Methods and/or figure legends, clarify what kind of ANOVA was performed, which groups are being compared and respective P values. In the Methods, provide as many details as required to understand the experimental design. More formally, ANOVAs are reported along with the F statistic and the degrees of freedoms. F(2, 8) = 42.659; P = 5.401e-05 for the one-way mixed effects analyses above.
We will use the data_t_pratio data set from grafify. Look at the variables and perform exploratory plots.
Plots of paired or matched data are also called before-after plots.
#example 1
plot_befafter_box(data_t_pratio,
xcol = Genotype,
ycol = Cytokine,
match = Experiment,
LogYTrans = "log10")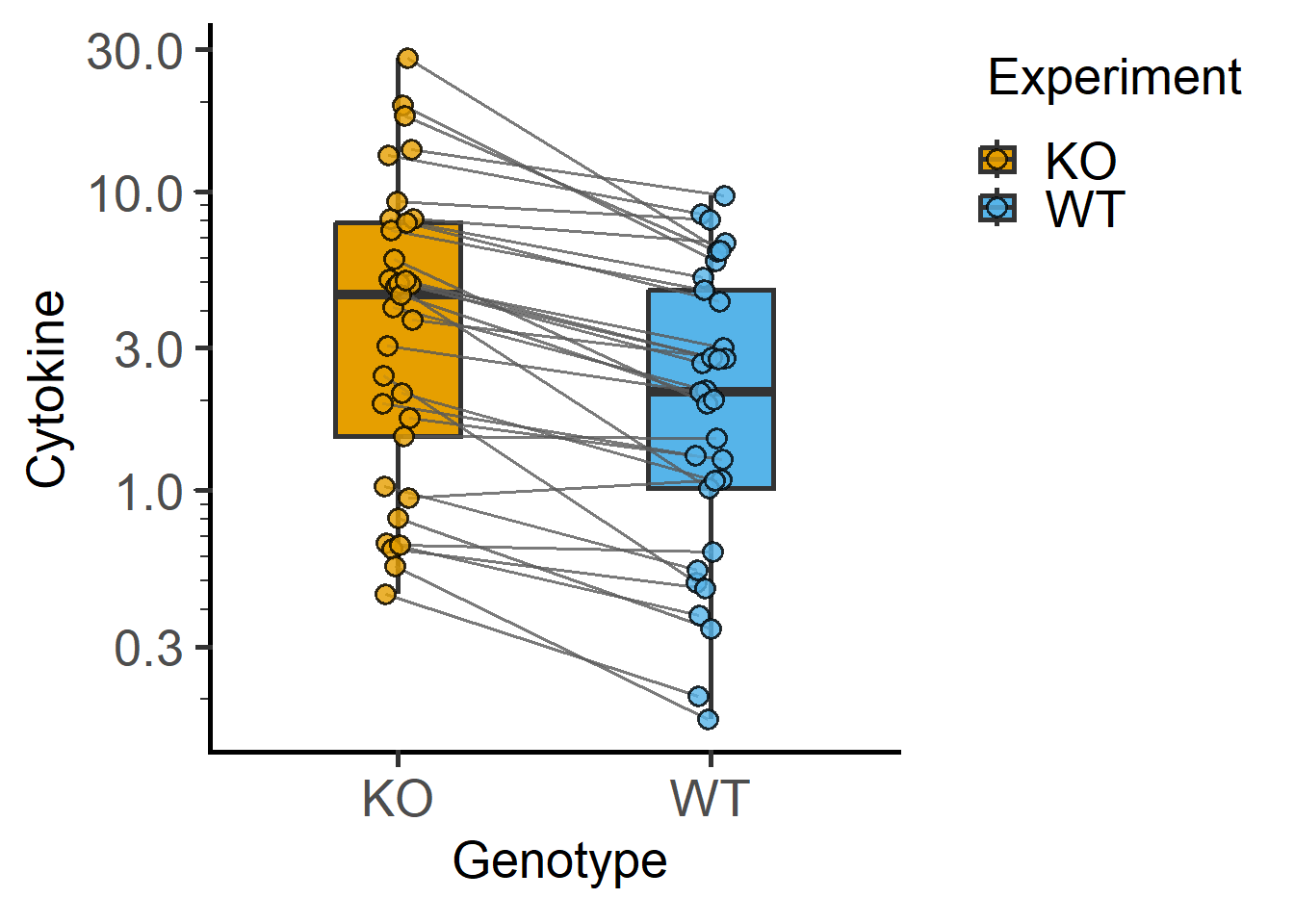
#example 2
plot_befafter_colors(data_t_pratio,
xcol = Genotype,
ycol = Cytokine,
match = Experiment,
Boxplot = TRUE,
LogYTrans = "log10")+
guides(fill = "none")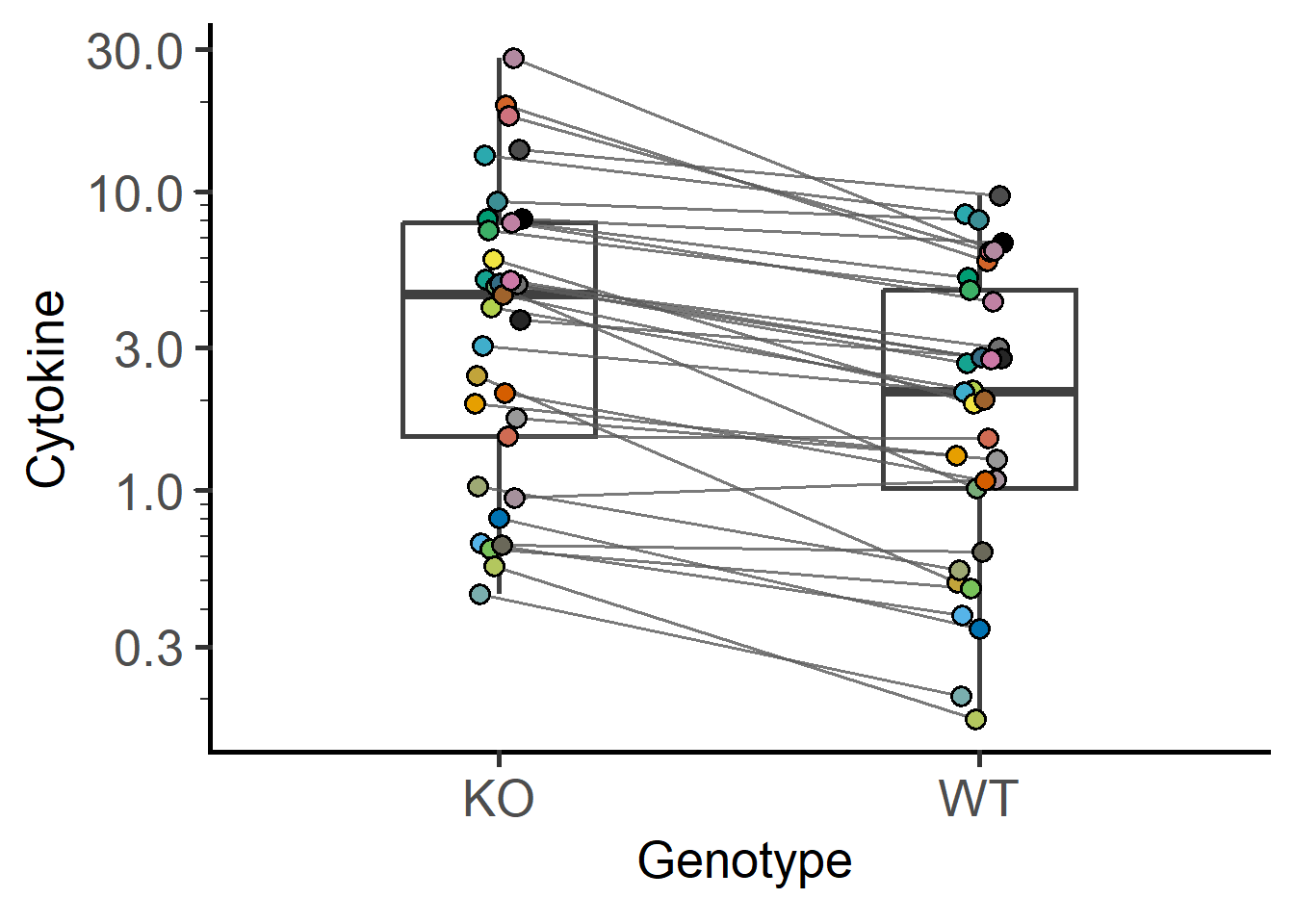
Let’s use a mixed effects linear model to compare these two groups.
The new argument `AvgRF` is set to TRUE by default in >=5.0.0). Response variable is averaged over levels of Fixed and Random factors. Use help for details.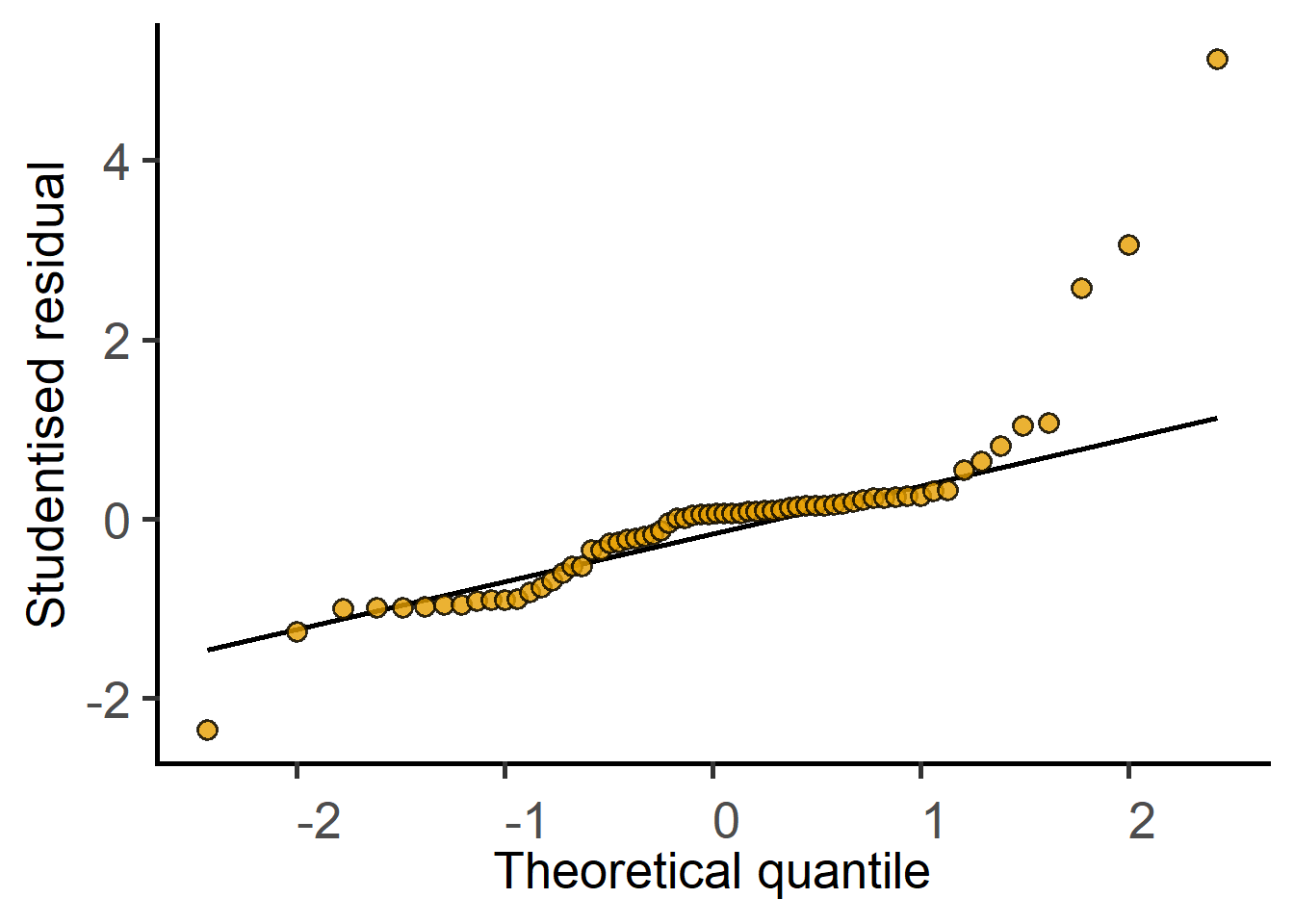
The QQ plot of residuals looks skewed. Should we consider data-transformation?
The new argument `AvgRF` is set to TRUE by default in >=5.0.0). Response variable is averaged over levels of Fixed and Random factors. Use help for details.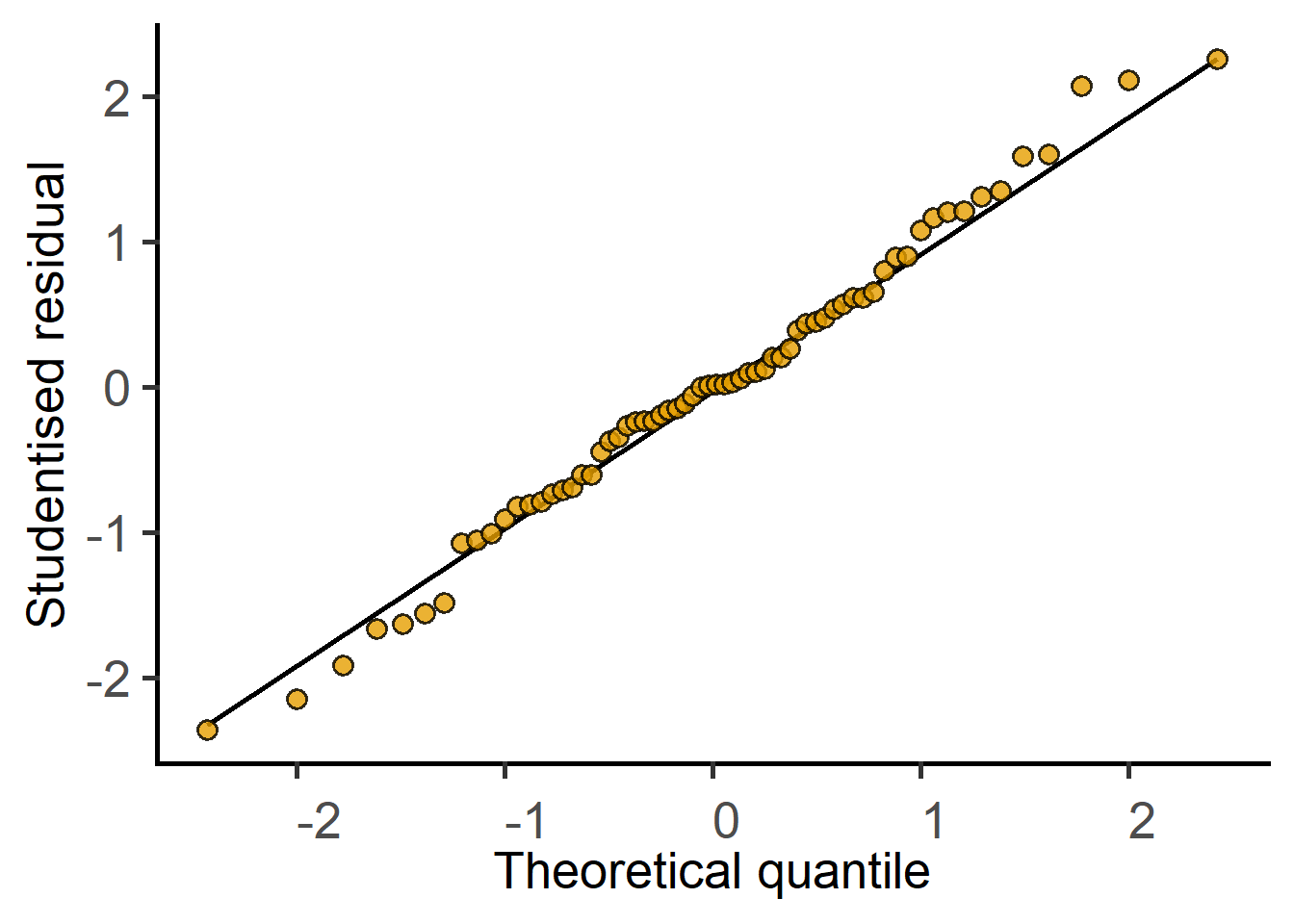
Use mixed_anova or summary to get the ANOVA table.
For paired t-tests to work with t.test correctly with long-format data tables, the order of paired data has to be the same for both groups.
When using t tests, check approximate normality of both groups first.
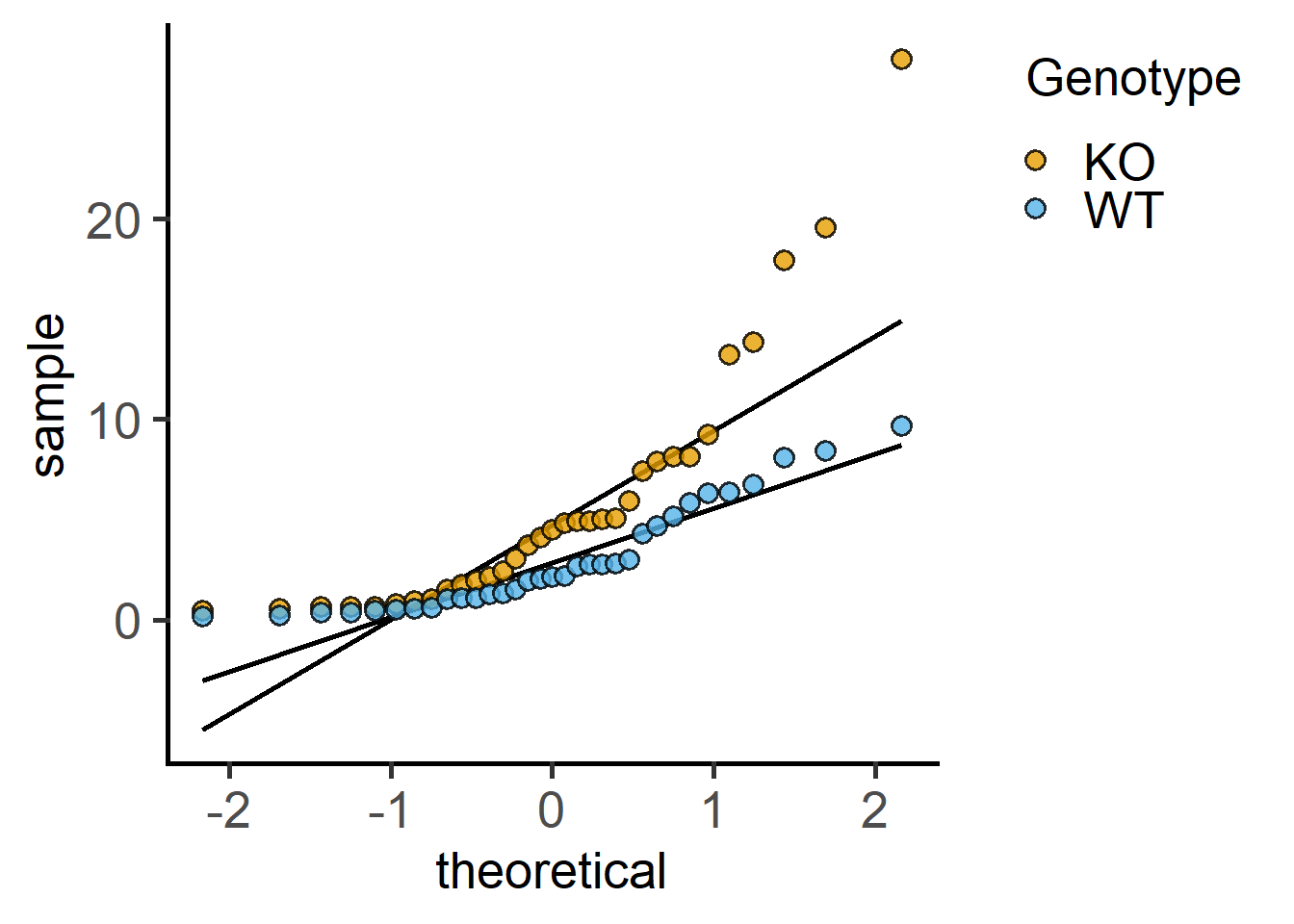
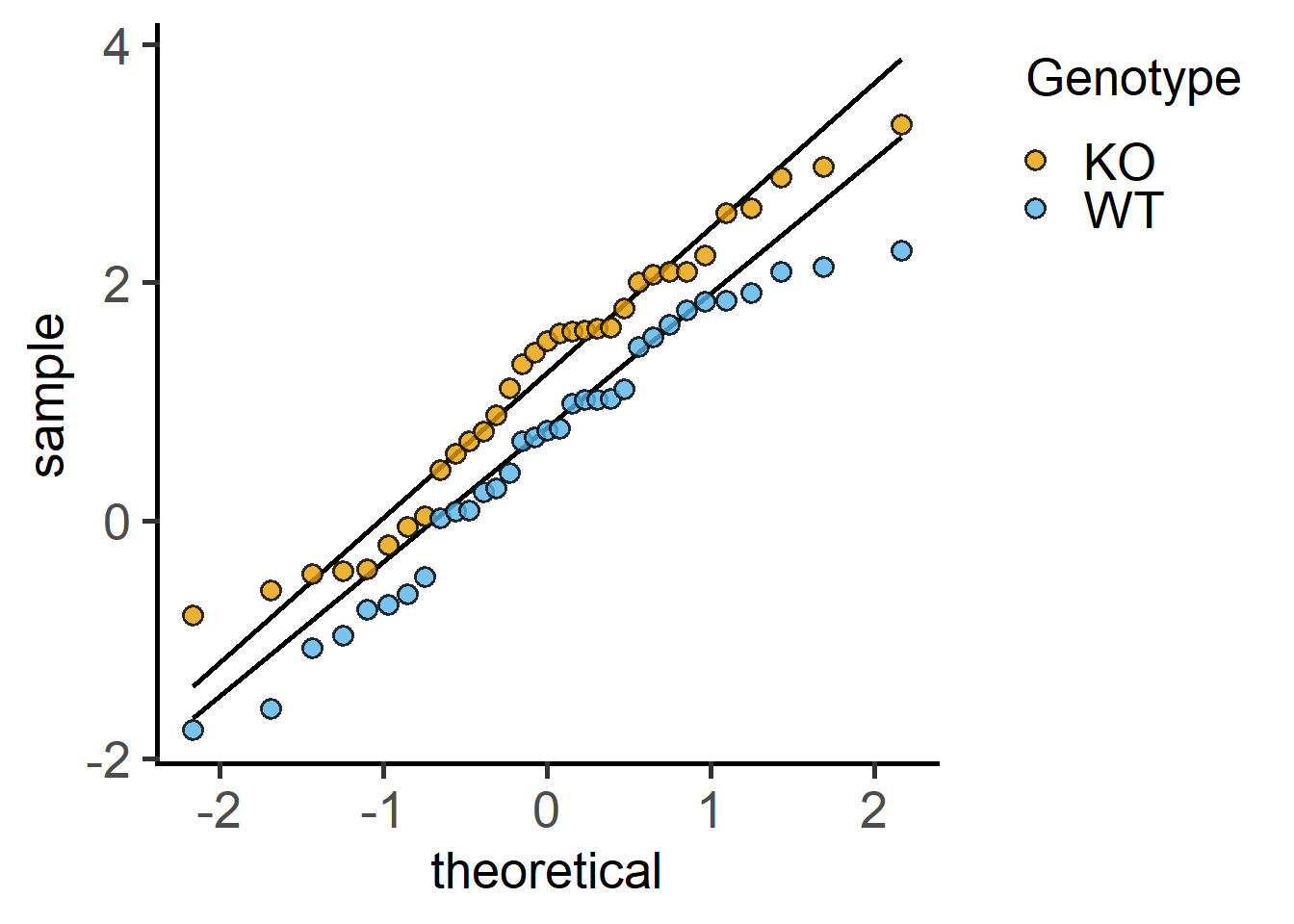
Proceed to the t test on the appropriately transformed data set. Without data transformation, a paired t test calculates the paired differences.
This only works with wide tables after a recent update to t.test. So convert a long table to wide if you want to use t.test, or use mixed_model as above.
#make wide table first
library(tidyr)
wdata_t_pratio <- pivot_wider(data_t_pratio,
values_from = Cytokine,
names_from = Genotype)
#paired-difference t-test
t.test(wdata_t_pratio$WT, wdata_t_pratio$KO,
paired = TRUE)
Paired t-test
data: wdata_t_pratio$WT and wdata_t_pratio$KO
t = -3.7385, df = 32, p-value = 0.0007256
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-4.523562 -1.332764
sample estimates:
mean difference
-2.928163 With log-transformations, it calculates paired ratios.
#paired ratio t-test
#on log-transformed data
t.test(log(wdata_t_pratio$WT), log(wdata_t_pratio$KO),
paired = TRUE)
Paired t-test
data: log(wdata_t_pratio$WT) and log(wdata_t_pratio$KO)
t = -8.299, df = 32, p-value = 1.758e-09
alternative hypothesis: true mean difference is not equal to 0
95 percent confidence interval:
-0.7808986 -0.4731092
sample estimates:
mean difference
-0.6270039 Many biological data are log-normally distributed. This can mean that the ratio between two group means changes consistently than the difference between them.
For paired ratio t-tests, the null hypothesis is that ratio of the two group means = 1. That is
However,
Therefore, calculations with log-transformed data can be carried out as usual t tests. The null hypothesis is now rephrased as: the difference between the log-transformed means = 0. In other words, to test whether the ratio of the raw (untransformed) means of the two groups is consistent, use paired t test on log-transformed data.